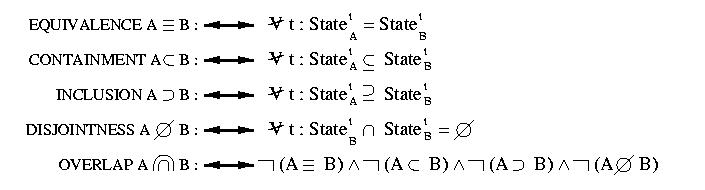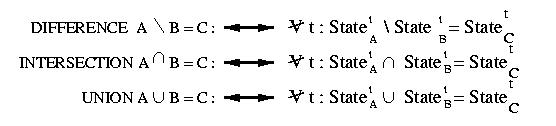METODOLOGIA PER IL CALCOLO DELLE BASE EXTENSION

Introduzione
I problemi incontrati cercando di implementare la metodologia proposta per il calcolo delle Base Extension sono :

Gli assiomi estensionali definiti dal progetista sono binari cioe' consentono di definire solamente relazioni tra due classi.Nel caso il progettista voglia dichiarare espressioni piu' complesse (Es. (A\B)=(C U D)) lo puo' fare solamente scomponendo l'espressione in piu' espressioni binarie e creando diverse classi temporanee.
Il calcolo delle Base Extension viene fatto utilizzando ODB-Tools , obbligando il programma ad una traduzione Estensionale/Intensionale e all'implementazione di vari controlli.
Non vi alcun tipo di supporto che aiuti il progettista nell'individuazione degli assiomi estensionali da inserire.

Il nuovo approccio che si vuole proporre per il calcolo delle Base Extension puo' essere schematizzato:

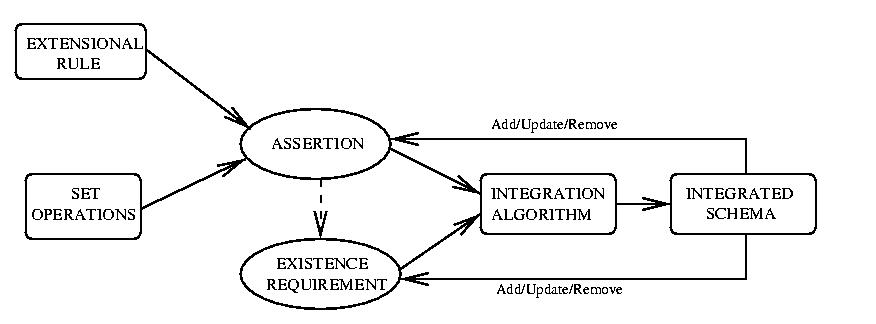
Il concetto di partenza su cui si basa questo approccio e' il fatto che e' estremamente improbabile che il progettista sia in grado di specificare inizialmente tutta la conoscenza estensionale, per questo e' stato studiato una metodologia che partendo da alcune informazioni permette di raggiungere il risultato voluto attraverso raffinamenti successivi.
Per permettere al progettista di esprimere relazioni n-arie trale varie classi oltre alle rule estensionali:

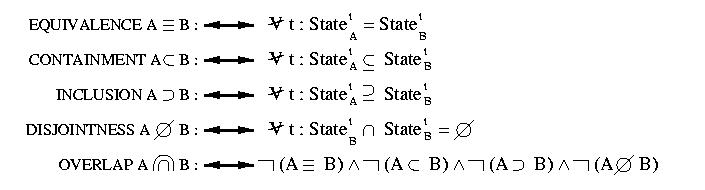
Vengono utilizzate anche le classiche operazioni tra insiemi :

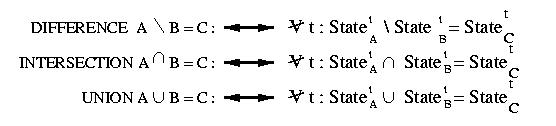
In questo modo il progettista e' in grado di specificare relazioni complesse (Assertions) tra le estensioni delle classi locali.

Algoritmo di calcolo

La parte iniziale dell'algoritmo puo' essere schematizzata :

A= a1,a2,....,an Insieme delle Assertion iniziali proposte dal progettista
ai -> ai(CNF)
Combino tutte le a1(CNF),a2(CNF),.....,an(CNF) in un unica espressione
Trasformo l'espressione del passo precedente in DNF

L'espressione ottenuta in DNF non rappresenta il nostro BES (Base Extension Set) perche' in ogni termine non vengono esplicitate tutte le variabili.
Esempio :
Suppongo di avere m classi c1,....,cm -> M= 2 exp m , Dim(M)=1024(Insieme che contiene tutte le possibili BE)

Definisco le assertion c1 overlap c2 , c3 equ c4

Ottengo DNF = c3c4 + not(c3)not(c4)

Da questa espressione non riesco a determinare il comportamento delle altre classi, per farlo devo avere tutte le 10 classi contenute in ogni termine.
Per poter ottenere un BES devo passare dalla DNF alla DCF (Disjunctive Canonical Form) cioe' preso M = 2 exp m estraggo solo i termini che verificano le assertion date.
Procedendo in questo modo si calcola un BES corretto ma ridondante cioe' contenenete molte BE che poi saranno vuote, inoltre la complessita' dell'algoritmo e' esponenziale , basti pensare che con l'esempio proposto ottengo (2* 2 exp 10) / 4 = 512 BE .
Partendo dall'espressione in DNF l'idea di fondo dell'algoritmo e' quella di non creare tutte le possibili BE che verificano le assertion ma di creare solo quelle BE che sono sicuramente popolate.

Existence Requirement
Un existence requirement e e' un espressione logica rappresentata da almeno una BE del BES.

Existence Requirement <-> State e^t <> 0

Date n assertion gli ER rappresentano un insieme di BE che sicuramente sono popolate.
Date 2 classi A,B

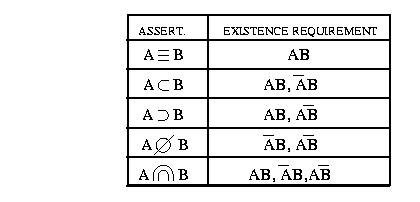
Partendo dalle assertion in DNF invece di considerare tutte le possibili BE che le verificano utilizzo gli existence requirement per creare un BES corretto e minimo,cioe' contenente il numero minimo di BE popolate.

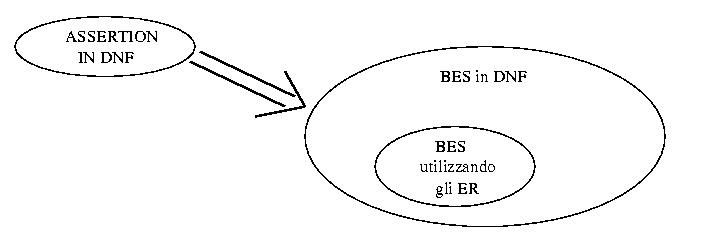
In questo modo riesco ad ottenere un insieme minimo di BE popolate, inoltre posso offrire al progettista la possibilita' di definire esplicitamente alcuni ER in situazioni particolari, offrendo la maggior flessibilita' possibile.

Implementazione

Partendo dalla espressione in CNF (non in DCF) costruisco la Source Table dove ogni riga corrisponde ad una classe ed ogni colonna e' un termine della nostra espressione in CNF.
ES.
Suppongo di avere 4 classi

Per ogni variabile (classe) non negata inserisco 1
Per ogni variabile (classe ) negata inserisco uno 0
Lascio vuoti i campi relativi alle variabili non specificate

Osservando questa tabella risulta ancora piu' chiaro il significato del passaggio dalla DNF alla DCF per il calcolo delle BE, dovrei completarla riempiendo i campi rimasti vuoti con tutte la possibili combinazioni compatibili con i valori presenti in partenza.Otterrei (2 exp 3)=8 combinazioni per la prima colonna e (2 exp 3)= 8 combinazioni per la seconda colonna per un totale di 16 BE .Vedremo che invece utilizzando gli ER riesco ad ottenere un BES molto piu' piccolo.

1. Creo una tabella vuota Target Table con 4 righe (una per variabile) e nessuna colonna.
2. Per ogni ER e specificato eseguo i passi :
2a. Se la Target Table soddisfa e passo al ER successivo.
2b. Prendo la prima colonna disponibile della Target Table che soddisfa e riempiendo alcuni campi vuoti con 1 o 0 (riempio solamente i campi strettamente necessari per soddisfare e).
2c. Prendo la prima colonna disponibile dalla Source Table e la riempio come al passo precedente.
3. Riempio tutti i campi rimasti con 0

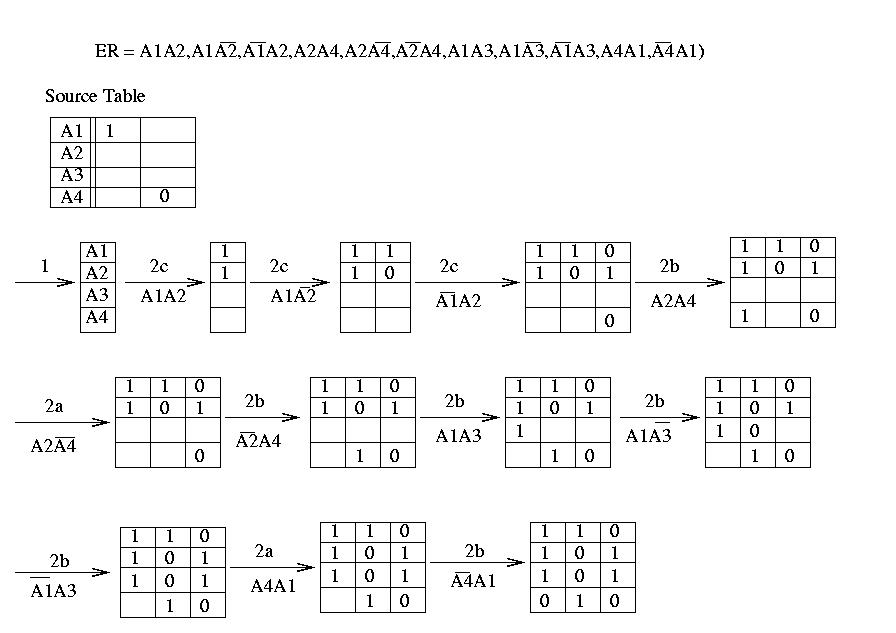
Al termine dell'algoritmo ho ottenuto solamente 3 BE che verificano le Assertion e gli ER e posso individuare 3 differenti stati :
1. L'algoritmo si e' bloccato perche' ho introdotto Assertion incogruenti (alcuni ER non verificano la Source Table) :
Se fossero definite le rule A
2.Ottengo il mio BES ma non e' quello corretto poiche' non rappresenta tutta la conoscenza estensionale.
2a.L'insieme delle Assertion e' incompleto o scorretto.
2b. L'insieme delle Assertion e' corretto ma l'insieme degli ER e' incompleto.
3. Il BES e' corretto e completo e rappresenta tutta la conoscenza estensionale.
Dal BES ottenuto tramite l'algoritmo riesco facilmente (applicando la teoria del formal context) a calcolate la gerarchia estensionale e da questa ricavare altre Assertion oppure apportare delle modifiche per poi applicare di nuovo l'algoritmo sopra descritto ovviamente utilizzando una Source Table arricchita delle informazioni aggiunte.In maniera iterativa ottengo per raffinazioni successive di passare dallo stato 1 o 2a allo stato 2b .Il passaggio dallo stato 2b al 3 e'immediato ,basta trasformare la Source Table nella corrispondente espressione in DNF.Il nostro problema quindi si riduce quindi a riuscire ad individuare quando l'algoritmo si trova nello stato 2b.
Un metodo per fare questo potrebbe essere quello di fissare un Upper Bound.
Date n classi il numero max diBE e' dato da (2 exp n)
Durante i primi cicli dell'algoritmo le informazioni estensionali inserite sono ancora insufficenti e questo si traduce in una Source Table con molti campi vuoti .

Mentre proseguendo iterativamente ed aggiungendo nuova conoscenza ad ogni ciclo arrivo ad ottenere una Source Table piu' completa.

Fissando un parametro alfa con 0<alfa<1 imposto un Upper Bound UB = alfa(2 exp n) .
Quando il numero di BE ottenute dalla Source Table e' < UB suppongo di trovarni nello stato 2b.
Osservazioni
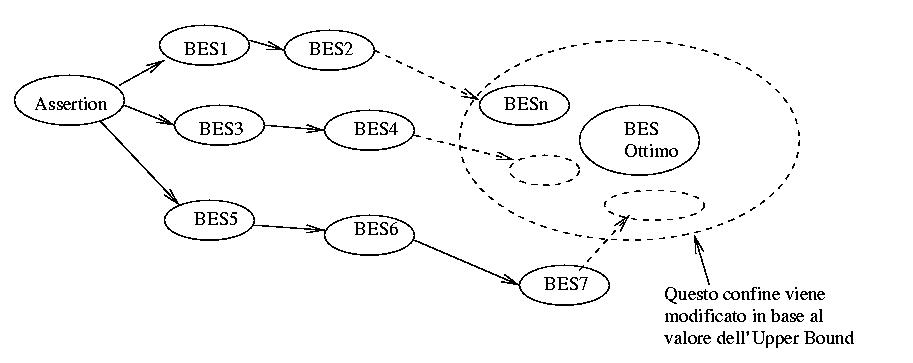
Il BES ottimo e'solamente uno ed e' estremamente difficile da individuare, io mi accontento di trovare un BES che si avvicina il piu' possibile a quello ottimo (nella situazione peggiore avro qualche BE ridondante ).
Sia nello stato 2a che nello stato 2b il BES puo' variare a seconda dell'ordine in cui io fornisco gli ER all'algoritmo , e' come se partendo da una data Source Table io potessi percorrere diversi percorsi che portano al BES ottimo, impostando un Upper Bound fisso una soglia di tolleranza entro la quale il mio BES e' onsiderato quello ottimo.

VANTAGGI

Insieme BES minimo

Rule n-arie

Non e' necessario l'impiego di ODB-Tools

Non occorre fare la traduzione Est/Int

Non occorre fare controlli sulle rule (rule equivalenza, ....)

Individuazione rule inconsistenti

Supporto al progettista per ottenere il BES tramite raffinazioni successive

Semplice implementazione del SW

SVANTAGGI

Traduzione espr. logica -> DNF,CNF

Ridefinizione della sintassi delle Assertion

Proposta di interfaccia grafica
Proposta per la fusione dei cluster